

This exploration looks at how spreadsheets can help us do quick and multiple iterations of calculations, in particular, I used Microsoft Excel.
The Fibonacci Sequence is a series of numbers where the next number is made up of the sum of the previous two numbers:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34,…
We can use Excel to quickly add up the numbers for us and look at relationships between the numbers. First we need a formula to use:
f(0) = 1, f(1) = 1,
f(n) = f(n-1) + f(n-2)
Inputting into Excel gave me this:
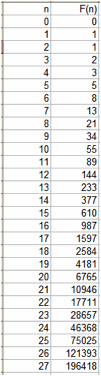
This means that the 25th term in the Fibonacci Sequence is 75,025.
Now, let’s examine the ratio of each adjacent term of the sequence:
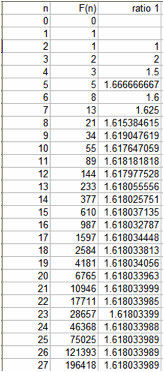
As n increases, the ratio gets closer and closer to the Golden Ratio φ
In other words, using larger values from the Fibonacci Sequence gives a closer approximation of the Golden Ratio.
Here is a look at the ratio of every 2nd, 3rd , and 4th terms:
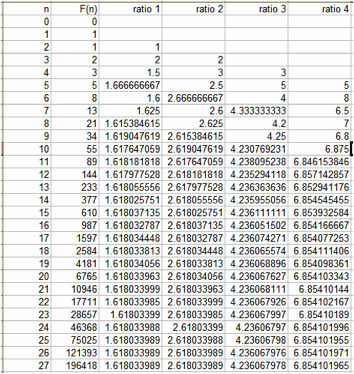
Looking at the pattern formed by the ratio it looks like the Fibonacci Sequence appears again, diagonally!
There also seems to be a pattern forming with the ratios, as the 4th column looks like it gets closer to the 3rd column plus 1, or (using the 27th term)
1.6180333989 + 1 = 2.618033989.
The 5th column looks like twice the 3rd column plus 1 as well, or (still using the 27th term) 2(1.618033989) + 1 = 4.236067978.
The 6th column must have a similar pattern and with some number manipulations, I found 3(1.618033989) + 2 = 6.854101966.
The Fibonacci Sequence again!
That would mean that the ratio formed by every 5th term can be found by:
5(1.618033989) + 3 = 11.09016994.
Here is the Excel spreadsheet with the Fibonacci Sequence and ratios, if needed.
What if we started with other numbers than 0 and 1
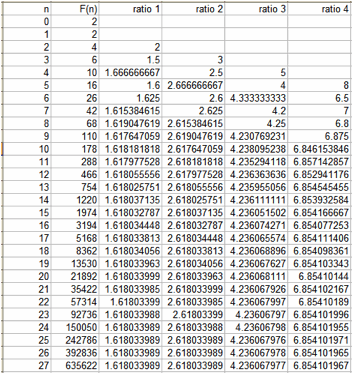
Here, I started with 2 and 2, and the ratios are almost identical to the ratios for the Fibonacci Sequence.
This sequence is called the Lucas Sequence.